Tenes dos funciones, y con cualquier mensaje al pasarlo por la función lo podes convertir en un mensaje sin sentido. Esto sirve si:
- Nadie conoce las funciones de encoding y decoding
- Las funciones son conocidas por todos pero aceptan otro parámetro, llamado clave, que mantenemos secreto para que el adversario no pueda descifrar el mensaje
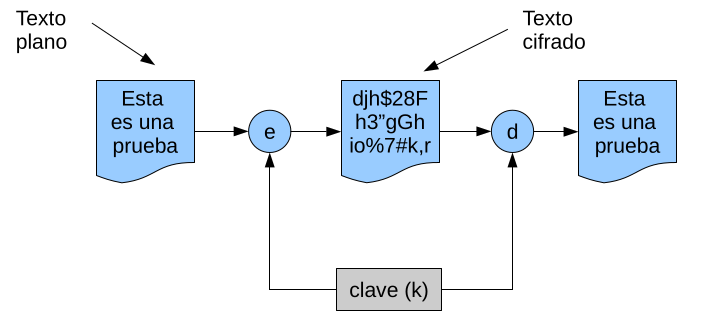
Un criptosistema debe ser seguro incluso si todo sobre el sistema, excepto la clave, es de publico conocimiento
- Principio de Kerckhoffs
Hay dos grandes aplicaciones para este tipo de criptografía: Comunicación entre dos personas físicamente separadas, donde se asume que la clave fue compartida anteriormente (Intercambio de Claves), y cuando una persona se quiere comunicar con sigo misma luego de un tiempo (por ejemplo, disk encryption), donde ahora compartir la clave es trivial, pues solo la debe conocer una persona, pero tiene que asegurarse una forma de recordarla o guardarla para utilizarla en el futuro.
Criptosistemas Históricos
Cifrado de Sustitución
Reemplaza un símbolo por otro, son identificables porque las propiedades estadísticas del lenguaje no se ven alteradas. Obteniendo la frecuencia estimada de cada símbolo en el lenguaje del mensaje, se calcula la frecuencia de cada símbolo en el texto cifrado, y asumiendo que los símbolos de mayor probabilidad se corresponden, tratamos de formar grupos de dos y tres letras comunes (el, la, de, las, los, etc en español)
Cifrado Vigenere
Es una substitution polialfabetica, dado que un mismo símbolo puede transformarse a diferentes. Se creyó por mucho tiempo que era seguro, porque destruye completamente las propiedades estadísticas del lenguaje del mensaje.
Para atacarlo, primero se debe determinar la longitud del bloque (la clave), y luego analizar la clave de cada bloque por separado. Aparecen n-gramas repetidos al transformar los mismos símbolos en la misma posición (Test de Kasiski):
- Buscar secuencias repetidas
- Calcular la distancia entre las secuencias
- La longitud de la clave es múltiplo del MCD entre las distancias halladas
Luego, determinamos estadísticamente las letras más probables en cada grupo, y estimamos las rotaciones que llevan a cada grupo a equipararse con las estadísticas del lenguaje. Probando las rotaciones, eliminamos caminos al encontrar combinaciones sin sentido.